Resultado de imagen de gifs animados de estudiantes y profesores

En esta sesión se trabajara con las paginas 52 - 55 del libro de matemáticas vamos a aprender de grado noveno.

Razones Trigonométricas en triángulos rectángulos

empiezan a hablarnos de razones trigonométricas… de senos, cosenos, tangentes… ¡Pero esto qué es ahora!

Resulta que los lados del triángulo rectángulo ya no tienen sólo nombres, sino que también tienen apellidos: cateto opuesto y cateto contiguo o adyacente.

Así, aprendemos que el seno de un ángulo α es la razón entre el cateto opuesto a dicho ángulo y la hipotenusa…

… el coseno de un ángulo α es la razón entre el cateto contiguo o adyacente a dicho ángulo y la hipotenusa…

… y la tangente de un ángulo α es la razón entre el seno de dicho ángulo y su coseno o, expresado de otra manera, entre el cateto opuesto y el cateto contiguo…

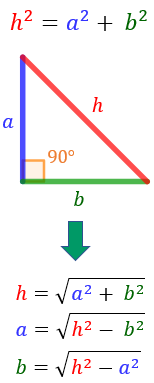
En los triángulos rectángulos se distinguen unos lados de otros. Así, al lado mayor de los tres y opuesto al ángulo de 90 grados se le llama hipotenusa, y a los otros dos lados catetos.

Pues bien, el Teorema de Pitágoras dice que: «En todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos«.

Resultado de imagen de teorema de pitagoras

INTERACTUA CON EL RECURSO

Razones trigonométricas de ángulos notables

Seno, coseno y tangente de 30° y 60°

Si dibujamos un triángulo equilátero $ABC$ , cada uno de sus tres ángulos mide $60^{o}$ y, si trazamos una altura del mismo, h, el ángulo del vértice $A$ por el que la hemos trazado queda dividido en dos iguales de $30^{o}$ cada uno. Recurriendo al Teorema de Pitágoras, tenemos que la altura es:

$\displaystyle h=\sqrt{I^{2}-\left ( \frac{I}{2} \right )^{2}}=\sqrt{\frac{3I^{2}}{4}}=\frac{\sqrt{3}}{2}I$

$\displaystyle cos \ 30^{o}=\frac{\frac{\sqrt{3}}{2}I}{I}=\frac{\sqrt{3}}{2} \ \ \ \ \ \ \ \ \ \ cos \ 60^{o}=\frac{\frac{I}{2}}{I}=\frac{1}{2}$

$\displaystyle tg \ 30^{o}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3} \ \ \ \ \ \ \ \ \ \ tg \ 60^{o}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\sqrt{3}$